Algebra und Geometrie

Eine Gerade lässt sich auf unterschiedliche Weise beschreiben bzw. darstellen. Es gibt

• die explizite Darstellung,
• die implizite Darstellung,
• die Parameterdarstellung und
• die Normalvektordarstellung.

Die explizite und implizite Darstellung wurden teilweise bereits im Abschnitt Lineare Gleichungssysteme erläutert.

Explizite Darstellung

Die explizite Darstellung einer linearen Gleichung lautet in Österreich

\begin{matrix} y &=& k \cdot x + d \\  f(x) &=& k \cdot x + d\end{matrix}

oder in Deutschland

y = mx + b .

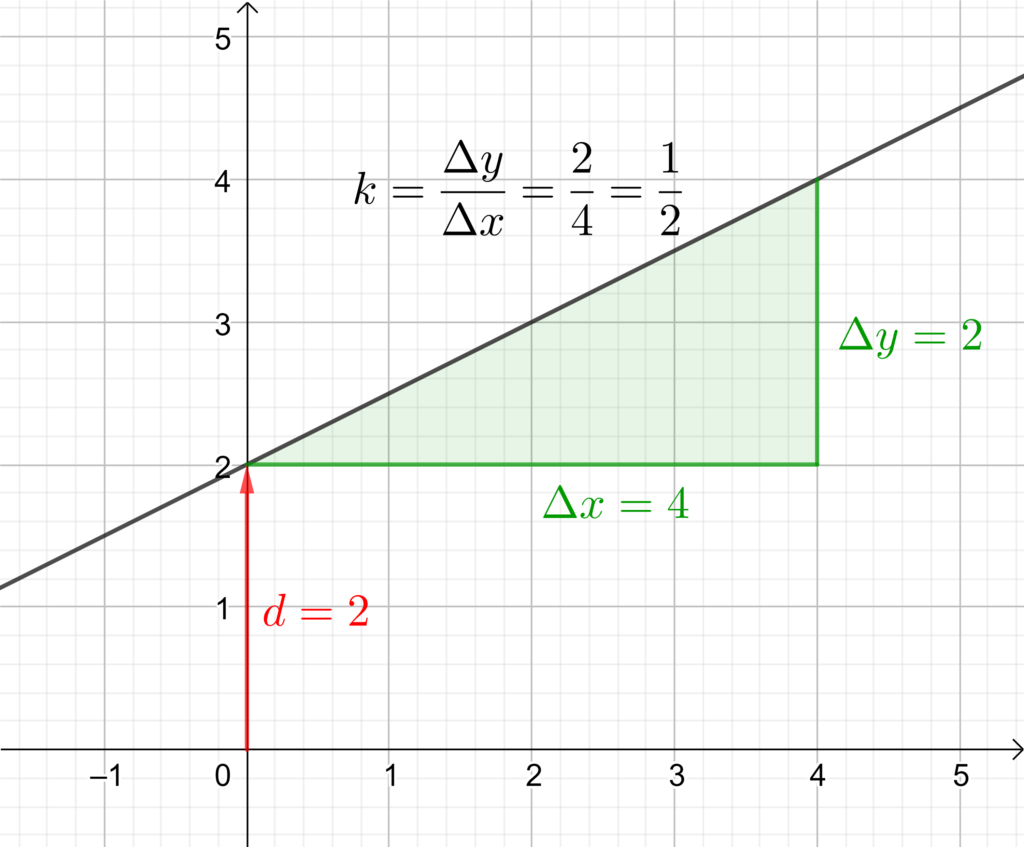
Wir gehen von der österreichischen Form aus. Dabei gibt der Wert von k die Steigung der Geraden an. Diese kann mit Hilfe des Differenzenquotienten

k = \dfrac{\Delta y}{\Delta x} = \dfrac{y_2 - y_1}{x_2 - x_1} = \dfrac{f(x_2) - f(x_1)}{x_2 - x_1}

In Worten bedeutet dies:

\text{Steigung} = \dfrac{\text{Änderung der Funktionswerte (y-Werte)}}{\text{Änderung der Argumente (x-Werte)}} = \text{durchschnittliche Änderungsrate}

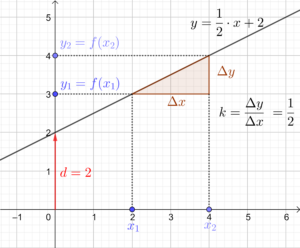
Die Wert von d gibt den sog. Achsenabschnitt an. Dieser Wert stellt den Schnittpunkt mit der y-Achse dar.  Ein Beispiel ist hier dargestellt. Man sucht sich zur Bestimmung zwei Punkte, die auf der Geraden liegen und bestimmt für zwei Argumente x_1, x_2 die zugehörigen Funktionswerte y_1 = f(x_1), y_2 = f(x_2) . Anschließend setzt man die Werte in die Gleichung zur Bestimmung der Steigung ein. Es ist dabei egal, welche Punkte man auswählt – für den Wert der Steigung erhält man stets denselben Wert. Den Achsenabschnitt d erhält man durch Ablesen des Schnittpunktes mit der y-Achse.

Parameterdarstellung

In der expliziten Darstellung erhalten wir alle Funktionswerte (y-Werte), indem wir alle Werte der Definitionsmenge (x-Werte) in die Gleichung einsetzen. Ähnlich gestaltet sich dies bei der Parameterdarstellung einer Gleichung. Allgemein sieht die Parameterdarstellung wie folgt aus:

\vec{x} = \vec{p} + \lambda \cdot \vec{v} mit \lambda \in \mathbb{R}

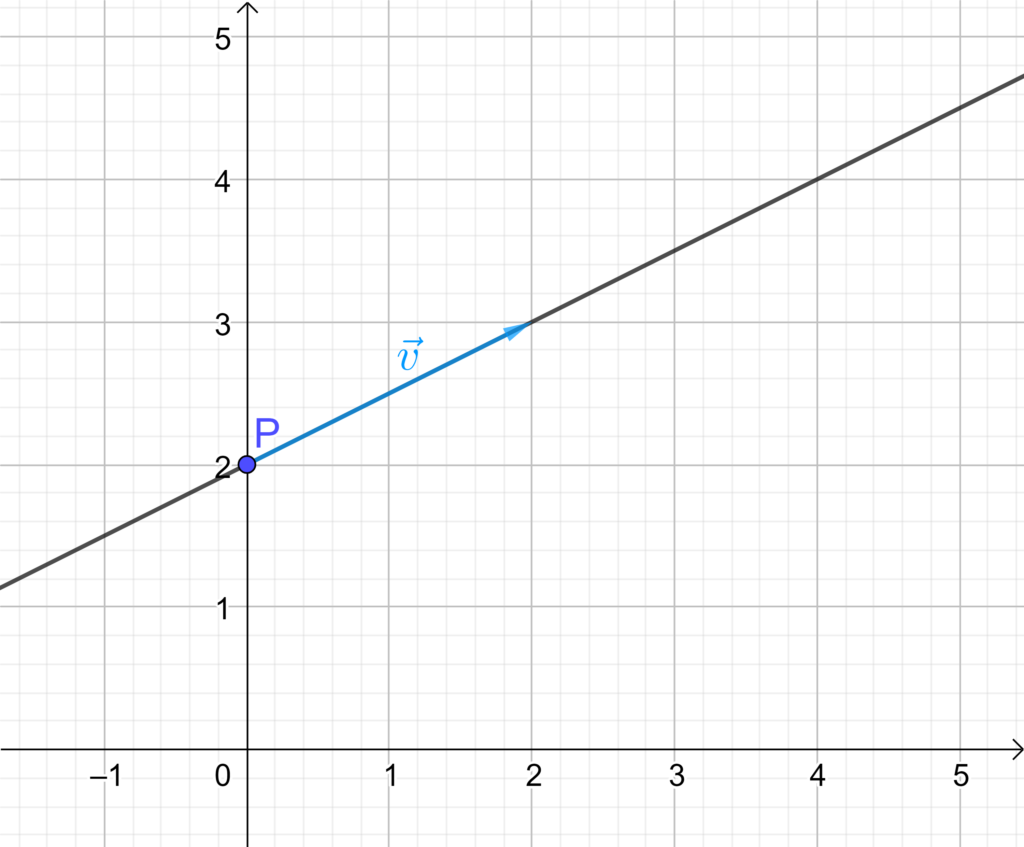
Der Ortvektor \vec{p} ist ein beliebiger Punkt, welcher auf der Geraden liegt. Der Vektor \vec{v} ist der Richtungsvektor der Geraden.

Wenn wir eine beliebige Gerade in der expliziten Darstellung betrachten, liegt der Punkt \left( \begin{matrix} 0 \\ d \end{matrix} \right) sicher auf der Geraden. Dies erkennt man auch an der oben dargestellten Abbildung. Zur Bestimmung des Richtungsvektors betrachten wir auch die obige Abbildung. Zur Bestimmung der Steigung haben wir uns zwei Punkte mit den Koordinaten \left( \begin{matrix} x_1 \\ y_1 \end{matrix} \right) und \left( \begin{matrix} x_2 \\ y_2 \end{matrix} \right) ausgesucht und daraus die Steigung berechnet. Wir können diese Punkte auch dazu verwenden den Richtungsvektor \vec{v} zu bestimmen. Wir rechnen wieder “Spitze minus Schaft”, um den Richtungsvektor zu bestimmen.

\vec{v} = \left( \begin{matrix} x_2 \\ y_2 \end{matrix} \right) - \left( \begin{matrix} x_1 \\ y_1 \end{matrix} \right) = \left( \begin{matrix} x_2 - x_1 \\ y_2 - y_1 \end{matrix} \right) = \left( \begin{matrix} \Delta x \\ \Delta y \end{matrix} \right)

Wir sehen also, dass sich auch hier die Werte wiederfinden, mit welchen wir die Steigung der Geraden bestimmt haben.

Wenn die Steigung der Geraden k = \dfrac{\Delta y}{\Delta x} ist, dann lautet der Richtungsvektor \vec{v} = \left( \begin{matrix} \Delta x \\ \Delta y \end{matrix} \right) und umgekehrt.

Dadurch kann man mit den Parametern der expliziten Geradengleichung die Gleichung der Parameterdarstellung wie folgt schreiben:

\vec{x} = \left( \begin{matrix} x \\ y \end{matrix} \right) = \left( \begin{matrix} 0 \\ d \end{matrix} \right) + \lambda \cdot \left( \begin{matrix} \Delta x \\ \Delta y\end{matrix}\right)

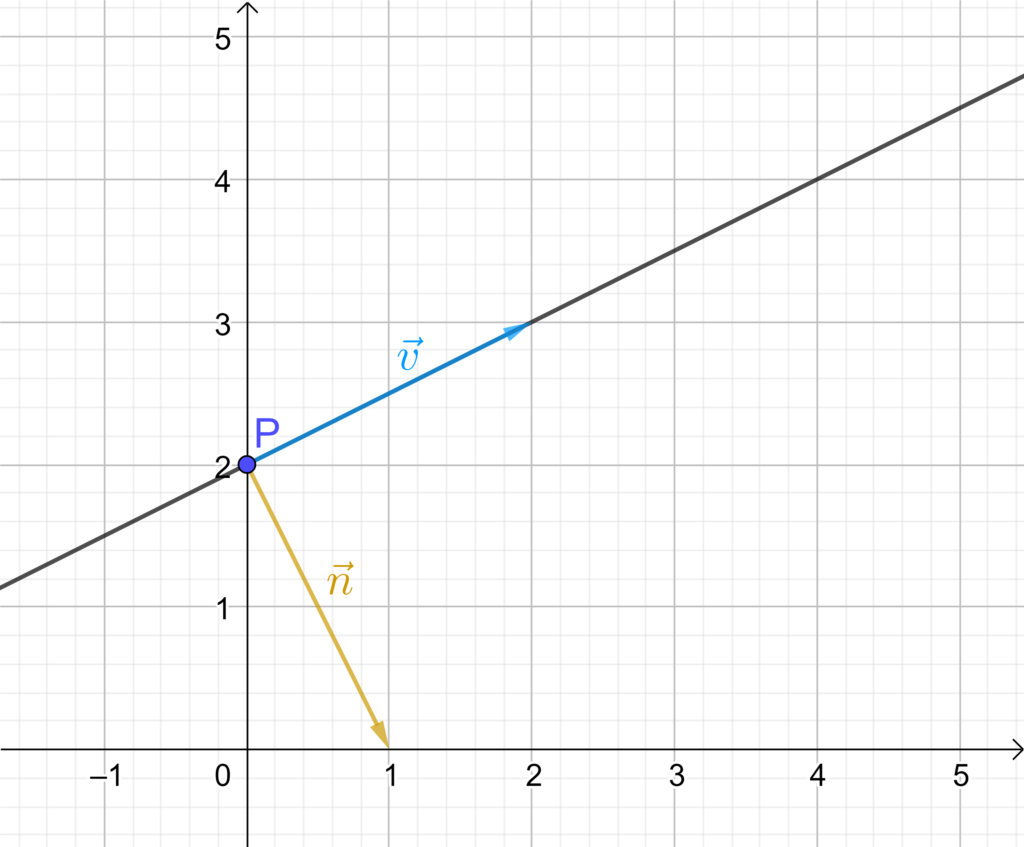
In der dargestellten Tabelle lassen sich die verschiedenen Geradendarstellungen finden. Außerdem sind die wichtigsten Zusammenhänge farblich gekennzeichnet – dies betrifft vor allem die Zusammenhänge zwischen der Steigung k , dem Richtungsvektor   \vec{v} und dem Normalvektor   \vec{n} .

Geradenform	Bild	Gleichung
Explizite Form		\begin{array}{rcccl} y &= &k &\cdot& x +d \\[1em] y &= &\dfrac{{\color{red}{\Delta y}}}{{\color{blue}{\Delta x}}} &\cdot& x + d \\[1em] y &= &\dfrac{{\color{red}{1}}}{{\color{blue}{2}}} &\cdot& x + 2 \end{array}
Parameterform		\begin{array}{rlcrrrc} \vec{x} &= &\vec{p} &+ &\lambda &\cdot &\vec{v} \\[1em] \left( \begin{matrix} x \\ y \end{matrix} \right) &= &\left( \begin{matrix} p_x \\ p_y \end{matrix} \right) &+ &\lambda &\cdot &\left( \begin{matrix} {\color{blue}{\Delta x}} \\ {\color{red}{\Delta y}}\end{matrix}\right) \\[1em] \left( \begin{matrix} x \\ y \end{matrix}\right) &= &\left( \begin{matrix} 0 \\ 2 \end{matrix} \right) &+ &\lambda &\cdot &\left( \begin{matrix} {\color{blue}{2}} \\ {\color{red}{1}}\end{matrix}\right) \end{array}
Normalvektorform		\begin{matrix} \vec{n} & \cdot & \vec{x} &=& \vec{n} &\cdot & \vec{p} \\[1em] \left( \begin{matrix}n_x \\ n_y \end{matrix}\right) & \cdot & \left( \begin{matrix}x \\ y \end{matrix}\right) &=& \left( \begin{matrix}n_x \\ n_y \end{matrix}\right) &\cdot &\left( \begin{matrix}p_x \\ p_y \end{matrix}\right) \\[1em] \left(\begin{matrix} {\color{red}{- \Delta y}} \\ {\color{blue}{\Delta x}}\end{matrix}\right) & \cdot & \left( \begin{matrix}x \\ y \end{matrix}\right) &=& \left(\begin{matrix} {\color{red}{-\Delta y}} \\ {\color{blue}{\Delta x}}\end{matrix}\right) &\cdot &\left( \begin{matrix}p_x \\ p_y \end{matrix}\right) \\[1em] \left(\begin{matrix} {\color{red}{-1}} \\ {\color{blue}{2}}\end{matrix}\right) & \cdot & \left( \begin{matrix}x \\ y \end{matrix}\right) &=& \left(\begin{matrix} {\color{red}{-1}} \\ {\color{blue}{2}}\end{matrix}\right) &\cdot &\left( \begin{matrix}0 \\ 2\end{matrix}\right) \\[1em] \left(\begin{matrix} {\color{red}{\Delta y}} \\ {\color{blue}{-\Delta x}}\end{matrix}\right) & \cdot & \left( \begin{matrix}x \\ y \end{matrix}\right) &=& \left(\begin{matrix} {\color{red}{\Delta y}} \\ {\color{blue}{-\Delta x}}\end{matrix}\right) &\cdot &\left( \begin{matrix}p_x \\ p_y \end{matrix}\right) \\[1em] \left(\begin{matrix} {\color{red}{1}} \\ {\color{blue}{-2}}\end{matrix}\right) & \cdot & \left( \begin{matrix}x \\ y \end{matrix}\right) &=& \left(\begin{matrix} {\color{red}{1}} \\ {\color{blue}{-2}}\end{matrix}\right) &\cdot &\left( \begin{matrix}0 \\ 2 \end{matrix}\right) \end{matrix}
Implizite Form		Aus der Normalvektorform erhält man durch Berechnung der Skalarprodukte \begin{matrix} &\underbrace{n_x}_a &\cdot &x& + &\underbrace{n_y}_b& \cdot& y& =& \underbrace{ p_x \cdot n_x + p_y \cdot n_y}_c &\\&\underbrace{{\color{red}{(-\Delta y)}}}_a &\cdot &x& + &\underbrace{{\color{blue}{\Delta x}}}_b& \cdot& y& =& \underbrace{ p_x \cdot {\color{red}{(-\Delta y)}} + p_y \cdot {\color{blue}{\Delta x}}}_c & \\& a& \cdot &x& + &b& \cdot &y& = &c& \\ &{\color{red}{-1}}& \cdot& x &+ &{\color{blue}{2}}& \cdot& y &= &(-1) \cdot 0 + (-2) \cdot 2& \\ &{\color{red}{-1}}& \cdot& x &+ &{\color{blue}{2}}& \cdot& y &= &-4& \end{matrix}