Die komplexen Zahlen

Da die beispielsweise die Gleichung x^2 = -1 im Rahmen der reellen Zahlen nicht gelöst werden kann, muss die Zahlenmenge zu den komplexen Zahlen \mathbb{C} erweitert werden.

In den reellen Zahlen kann man mit einem Ausdruck wie “\sqrt{-1} ” nichts anfangen, da Wurzel nur dann definiert sind, wenn der Radikant (so heißt der Wert unter der Wurzel) größer oder gleich Null ist.

Definition

Man definiert sich die imaginäre Einheit mit i^2 = -1 . (In der Elektrotechnik wird auch häufig der Buchstabe j verwendet.)

Deswegen kann man auch schreiben: i = \sqrt{-1 }.

Damit kann man auch die Gleichung x^2 = -1 lösen. Die Lösungen sind x_1 = -i und x_2 = i, da i^2 = -1 und (-i)^2 = (-1)^2 \cdot i^2 = i^2 =-1 gilt.

In den komplexen Zahlen \mathbb{C} sind eine Erweiterung der reellen Zahlen. Jede reelle Zahl ist daher auch eine komplexe Zahl. Dies führt auch gleich zur allgemeinen Darstellung einer komplexen Zahl. Meist werden komplexe Zahlen mit dem Buchstaben z geschrieben.

z = a + b \cdot i, wobei a, b \in \mathbb{R}

Jede komplexe Zahl z besteht aus den Realteil a und dem Imaginärteil b . Falls b = 0 ist, handelt es sich um eine reelle Zahl.

Beispiel

Wie sieht es aber nun mit anderen Aufgaben aus.  Gib die Lösungen der Gleichung x^2 = -2 .

Wir versuchen die Gleichung so umzuformen, dass wir unsere imaginäre Einheit verwenden können.

Darstellung

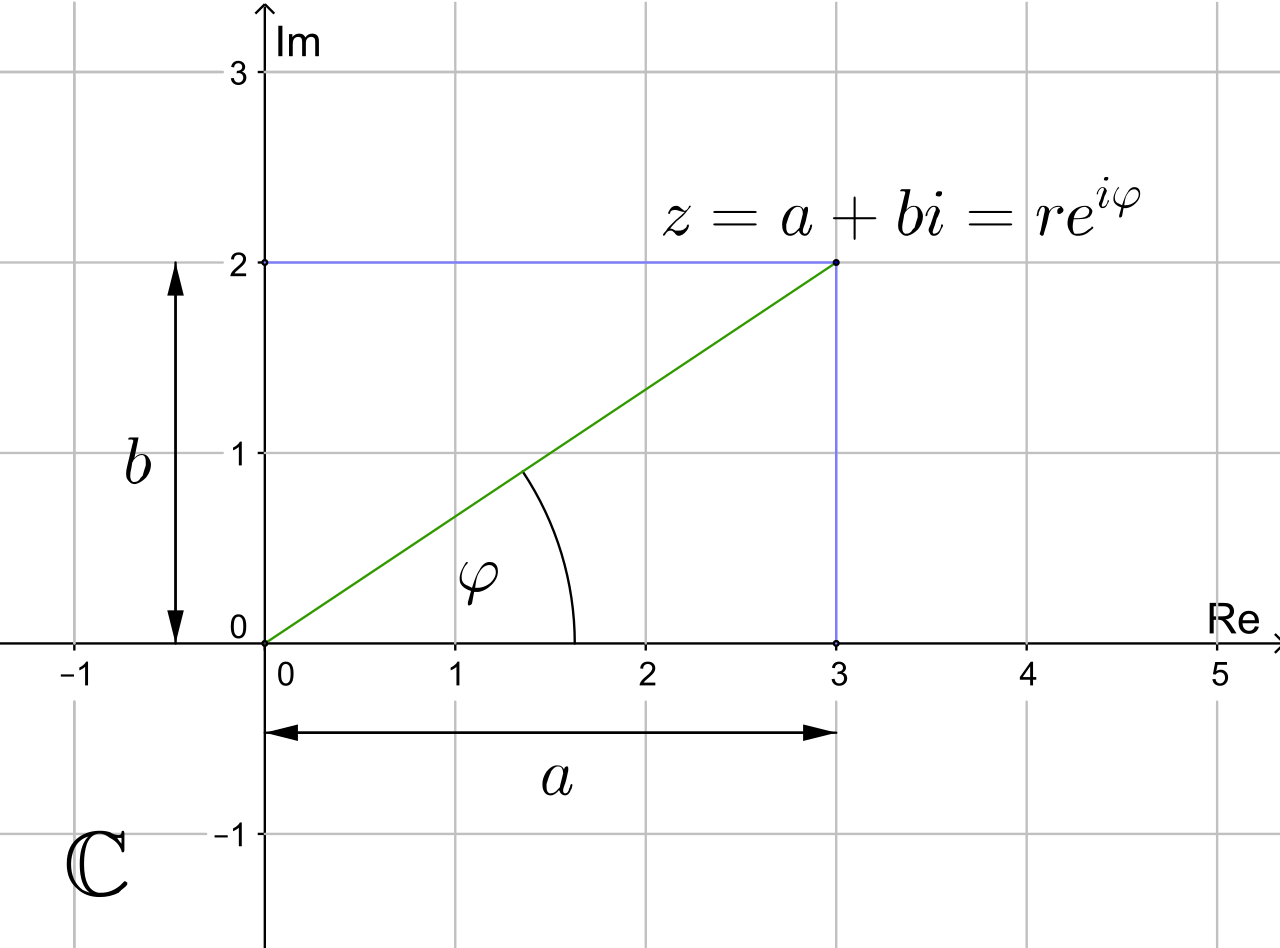
Die reellen Zahlen haben wir auf einem Zahlstrahl darstellen können. Da wir aber 2 Zahlen a, b benötigen, um eine komplexe Zahl anzugeben, müssen wir die komplexen Zahlen auch in 2 Dimensionen darstellen. Komplexe Zahlen werden in der sogenannten Gauß’schen Zahlenebene dargestellt. Die y-Koordinate gibt den Imaginärteil, also b , an und die x-Koordinate, also a , gibt den Realteil an. Ein komplexe Zahl stellt dann einen Punkt in dieser Ebene mit den Koordinaten (a,b) dar.

Zu den komplexen Zahlen gibt es noch sehr viel mehr zu sagen, aber dies sollte im Rahmen dieses Kurses für die Matura ausreichen. Ein guter Überblick liefert Wikipedia.