Wir haben im Abschnitt Was ist ein Vektor? gesehen, dass alle Pfeile, die

• gleich lang,
• parallel und
• gleichorientiert sind, denselben Vektor darstellen.

Aus diesem Grund kann man beiden Vektorschäfte (Anfänge beider Vektoren) in denselben Punkt verschieben. Dadurch kann man den Winkel, den zwei Vektoren einschließen bestimmen.

 

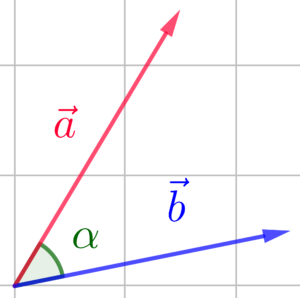
Den Winkel \alpha zwischen den zwei Vektoren \vec{a} und \vec{b} kann man mit folgender Bestimmungsgleichung ermitteln:

\cos \alpha = \dfrac{\vec{a} \cdot \vec{b}}{|\vec{a}| \cdot |\vec{b}|}

Wie kommt man auf diese Bestimmungsgleichung?

Um die Bestimmungsgleichung \cos \alpha = \dfrac{\vec{a} \cdot \vec{b}}{|\vec{a}| \cdot |\vec{b}|} benötigen wir 3 Eigenschaften bzw. Identitäten:

 

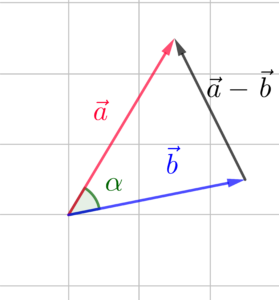
1. Cosinussatz: |\vec{a} - \vec{b}|^2 =  |\vec{a}|^2 + |\vec{b}|^2 - 2\cdot |\vec{a}| \cdot |\vec{b}| \cdot \cos \alpha . Der Cosinussatz stellt eine Verallgemeinerung des Satzes von Pythagoras dar, welcher bekanntlich nur in rechtwinkeligen Dreiecken gültig ist.

 

2. |\vec{a} - \vec{b}|^2 = (\vec{a} - \vec{b})^2

Beweis:

\begin{array}{rl} |\vec{a} - \vec{b}|^2 &= \left(\sqrt{(a_1 - b_1)^2 + (a_2 - b_2)^2}\right)^2 = (a_1 - b_1)^2 + (a_2 - b_2)^2 \\  (\vec{a} - \vec{b})^2 &= (\vec{a} - \vec{b}) \cdot (\vec{a} - \vec{b}) = \left( \begin{matrix} a_1 - b_1 \\ a_2 - b_2 \end{matrix} \right)  \cdot \left( \begin{matrix} a_1 - b_1 \\ a_2 - b_2 \end{matrix} \right) =  (a_1 - b_1)^2 + (a_2 - b_2)^2 \\ \Rightarrow |\vec{a} - \vec{b}|^2 &= (\vec{a} - \vec{b})^2  \end{array}

 

3. |\vec{a}|^2 = \vec{a}^2   bzw. |\vec{b}|^2 = \vec{b}^2

Beweis:

\begin{array}{rl} |\vec{a}|^2 &= \left( \sqrt{a_1^2 + a_2^2}\right)^2 = a_1^2 + a_2^2 \\[1em] \vec{a}^2 &= \vec{a} \cdot \vec{a} = a_1^2 + a_2^2  \\[1em] \Rightarrow  |\vec{a}|^2 &= \vec{a}^2\end{array}

Nun zur eigentlichen Herleitung. Wir gehen vom Cosinussatz aus und ersetzen die Ausdrücke durch die Identitäten 2 und 3. Dadurch erhalten wir

\begin{array}{rl} |\vec{a} - \vec{b}|^2 &=  |\vec{a}|^2 + |\vec{b}|^2 - 2\cdot |\vec{a}| \cdot |\vec{b}| \cdot \cos \alpha \\ (\vec{a} - \vec{b})^2 &= \vec{a}^2 + \vec{b}^2 - 2\cdot |\vec{a}| \cdot |\vec{b}| \cdot \cos \alpha  \\ \vec{a}^2 - 2 \cdot \vec{a} \cdot \vec{b} + \vec{b}^2 &= \vec{a}^2 + \vec{b}^2 - 2\cdot |\vec{a}| \cdot |\vec{b}| \cdot \cos \alpha \\ - 2 \cdot \vec{a} \cdot \vec{b} &= - 2\cdot |\vec{a}| \cdot |\vec{b}| \cdot \cos \alpha \\ \Rightarrow \cos \alpha &= \dfrac{\vec{a} \cdot \vec{b}}{|\vec{a}| \cdot |\vec{b}|} \end{array}

Lagebeziehung von Vektoren

Anhand der hergeleiteten Bestimmungsgleichungen lassen sich zwei wichtige Eigenschaften  in Bezug auf die Lagebeziehung von Vektoren ablesen. Wir verwenden dazu den umgeformten Ausdruck

\vec{a} \cdot \vec{b} = |\vec{a}| \cdot |\vec{b}| \cdot \cos \alpha 

Wir gehen davon aus, dass für die Vektoren \vec{a} \, \text{und} \,  \vec{b} Folgendes gilt: |\vec{a}| > 0 \, \text{und} \, |\vec{b}| > 0. Dies bedeutet, dass die Vektoren eine Ausdehnung haben, also kein Punkt sind.

1. Vektoren sind parallel

Wenn Vektoren parallel sind, dann ist der Ausdruck \vec{a} \cdot \vec{b}  maximal, da für den Winkel \alpha = 0 \, \cos \alpha = \cos 0 = 1.

2. Vektoren sind orthogonal (stehen normal aufeinander)

Wenn die Vektoren normal aufeinander stehen, dann gilt für den Winkel \alpha = 90^\circ . Dann folgt, dass \cos 90^\circ = 0 und mit der Bestimmungsgleichung \vec{a} \cdot \vec{b} = |\vec{a}| \cdot |\vec{b}| \cdot \cos \alpha  gilt, dass

\vec{a} \cdot \vec{b}  = 0   .

Allgemein gilt:

\vec{a} \cdot \vec{b}  = 0   \Leftrightarrow \vec{a} \perp\vec{b}

Wie findet man orthogonale Vektoren (= Vektoren, die normal/ senkrecht aufeinander stehen)?

Angenommen wir haben einen Vektor \vec{a} = \left( \begin{matrix} a_1 \\ a_2  \end{matrix} \right) gegeben und wollen die Komponenten des Vektors

\vec{b} = \left( \begin{matrix}  b_1 \\ b_2 \end{matrix} \right) bestimmen, sodass beide normal aufeinander stehen. Damit die Vektoren normal aufeinander stehen, muss das Skalarprodukt der beiden Vektoren 0 ergeben.

\vec{a} \cdot \vec{b}  = \left( \begin{matrix} a_1 \\ a_2  \end{matrix} \right) \cdot \left( \begin{matrix}  b_1 \\ b_2 \end{matrix} \right) =a_1 \cdot b_1 + a_2 \cdot b_2 =0  

Es muss also gelten:

a_1 \cdot b_1 + a_2 \cdot b_2 = 0  

Dies ist genau dann der Fall, wenn wir für b_1 = a_2   und b_2 = -a_1 wählen. Wir überprüfen dies:

   a_1 \cdot \underbrace{b_1}_{a_2} + a_2 \cdot  \underbrace{b_2}_{-a_1} =   a_1 \cdot a_2 - a_2 \cdot a_1 =   a_1 \cdot a_2 - a_1 \cdot a_2 = 0 \; \checkmark

Wir haben also einen Algorithmus gefunden, sodass wir zu einem gegeben Vektoren \vec{a} = \left( \begin{matrix} a_1 \\ a_2  \end{matrix} \right) einen Normalvektor \vec{b} = \left( \begin{matrix}  a_2 \\ -a_1\end{matrix} \right)   bzw. \vec{b} = \left( \begin{matrix}  - a_2 \\ a_1\end{matrix} \right) finden.

Um einen Normalvektor in \mathbb{R}^2 zu finden, vertauschen wir die Komponenten des Vektors und verändern bei einer Komponente das Vorzeichen.