Was ist ein lineares Gleichungssystem (LGS)?

Ein lineares Gleichungssystem besteht aus mehreren Gleichungen mit mehreren Variablen. Im Beispiel sind 3 Gleichungen mit den 3 Variablen x,y und z gegeben.

\begin{matrix} 3x & + & 2y & - & z & = & 1\\ 2x & - & 2y& + & 4z & = & -2\\ -x& + & {1 \over 2}y & - & z & = & 0 \end{matrix}

 

Was ist das Ziel?

Es ist das Ziel eines lineares Gleichungssystems, dass man für die Variablen (im Beispiel: x,y und z ) Werte findet, sodass alle Gleichungen gleichzeitig erfüllt sind. Im Beispiel wäre eine solch eine Lösung:

x = 1, y = -2, z = -2 . Dies kannst du überprüfen, wenn du diese Werte in die Gleichungen einsetzt.

Lineare Gleichungen mit 2 Variablen

Häufig hast du es in der Schule mit lineare Gleichungen in 2 Variablen zu tun. Wie du lineare Gleichungen aufstellen kannst, haben wir schon in der Lektion Lineare Gleichungen gesehen.

Jedes lineare Gleichungssystem kann (durch Umformen) in folgende Gestalten gebracht werden:

Allgemeine Form

x,y   sind Variablen.

a_1, a_2, b_1, b_2, c_1, c_2 sind reelle Zahlen.

\begin{matrix} \text{I:} & a_1 \cdot x & + & b_1 \cdot y &  = & c_1\\ \text{II:} & a_2 \cdot x &  + & b_2 \cdot y&  = & c_2 \end{matrix}

Normalform

x,y   sind Variablen.

k_1, k_2 sind die Steigungen der Geraden, also reelle Zahlen.

d_1, d_2 sind die Schnittpunkte mit der y-Achse, also auch reelle Zahlen.

\begin{matrix} \text{I:} & y & = & k_1 \cdot x + d_1 \\ \text{II:} & y & = & k_2\cdot x + d_2 \\ \end{matrix}

Übergang von der einen in die andere Form

Eine Gleichung in der allgemeinen Form kann in die Normalform umgewandelt werden und umgekehrt.

\begin{array}{rlll}6x + 2y &=& 12 & \; \text{allgemeine Form} \\ 6x + 2y &=& 12 &|  -6x\\2y &=&12 - 6x &| :2\\ y &=& \dfrac{12-6x}{2} &| \text{(Bruch auseinanderziehen und kürzen)} \\ y &=& 6-3x & \\ y &=& -3x + 6 & \; \text{Normalform}\end{array}

 

Lösungsfälle

	Eine Lösung	keine Lösung	unendlich viele Lösungen
Grafik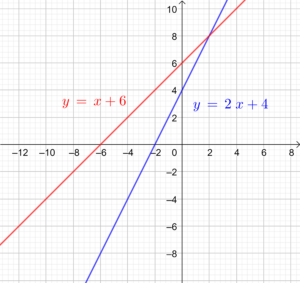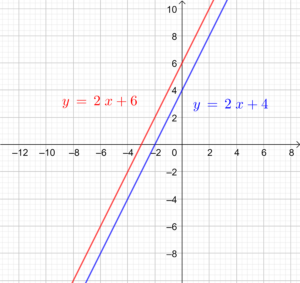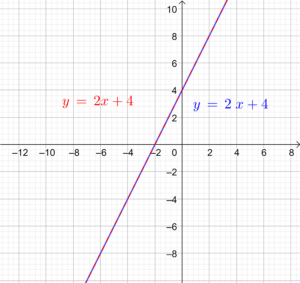
Beschreibung	Geraden schneiden sich	Geraden sind parallel	Gerade sind ident
Eine mögliche allgemeine Gleichung	\begin{matrix} \color{red}{\text{I:}}& -x &+& y &= &6 \\ \color{blue}{\text{II:}}& -2x &+& y &=&4 \end{matrix}	\begin{matrix} \color{red}{\text{I:}}&-4x &+& 2y &= &12 \\ \color{blue}{\text{II:}}&-2x &+& y &=&4 \end{matrix}	\begin{matrix} \color{red}{\text{I:}}&-4x &+& 2y &= &8 \\ \color{blue}{\text{II:}}&-2x &+& y &=&4 \end{matrix}
Normalform	\begin{matrix} \color{red}{\text{I:}}& y & = & x & + & 6\\ \color{blue}{\text{II:}}&y & = & 2x & + & 4 \end{matrix}	\begin{matrix} \color{red}{\text{I:}}& y & = & 2x & + & 6\\ \color{blue}{\text{II:}}&y & = & 2x & + & 4 \end{matrix}	\begin{matrix} \color{red}{\text{I:}}& y & = & 2x & + & 4\\ \color{blue}{\text{II:}}&y & = & 2x & + & 4 \end{matrix}
Lösungsmenge	\mathbb{L} = \{(2,8)\}	\mathbb{L} = \{\}	\mathbb{L} = \{(x,y) | \, y = 2x+4\}

Lösungsfälle anhand der Normalform unterscheiden

Eine Lösung

In der Normalform äußert sich eine Lösung darin, dass die beiden Gleichungen unterschiedliche Steigungen haben. Es gilt also: k_1 \neq k_2 . Die Werte der Achsenabschnitte d_1, d_2 sind dabei egal.

Keine Lösung

In der Normalform äußert sich keine Lösung darin, dass die beiden Gleichungen gleiche Steigungen haben (k_1 = k_2) und die Werte der Achsenabschnitte unterschiedlich sind, also d_1 \neq  d_2 .

Unendlich viele Lösungen

In der Normalform äußern sich unendlich viele Lösungen darin, dass die beiden Gleichungen gleiche Steigungen haben (k_1 = k_2 ) und Werte der Achsenabschnitte auch gleich sein müssen (d_1 = d_2 ).

Lösungsfälle anhand der allgemeine Form unterscheiden

Keine Lösung

Wenn du die linke Seite der Gleichung \text{I} mit einer Zahl multiplizierst oder dividierst und dann die linke Seite der Gleichung \text{II} erhältst, dann sind die Geraden entweder parallel (keine Lösung) oder identisch. Wenn du die rechte Seite der Gleichung \text{I} mit einer anderen Zahl multiplizieren musst, um auf die rechte Seite der Gleichung \text{II} zu kommen, so gibt es keine Lösung.

\begin{matrix} \color{red}{\text{I:}}&-4x &+& 2y &= &12\\ \color{blue}{\text{II:}}&-2x &+& y &=&4 \end{matrix}

In diesem Beispiel gilt: \dfrac{1}{2} \cdot {\color{red}{\text{(linke Seite I)}}} = \color{blue}{\text{(linke Seite II)}} .

Aber: \dfrac{1}{3} \cdot {\color{red}{\text{(rechte Seite I)}}} = \color{blue}{\text{(rechte Seite II)}} und \dfrac{1}{3} \neq \dfrac{1}{2} . Es gibt also keine Lösung.

Unendlich viele Lösungen

Wenn du die linke und die rechte Seite der Gleichung \text{I} mit derselben Zahl  mulitplizierst oder dividierst und dann die Gleichung \text{II} erhältst, so gibt es unendlich viele Lösungen.

\begin{matrix} \color{red}{\text{I:}}&-4x &+& 2y &= &8\\ \color{blue}{\text{II:}}&-2x &+& y &=&4 \end{matrix}

In diesem Beispiel gilt: \frac{1}{2} \cdot {\color{red}{\text{I}}} = \color{blue}{\text{II}} .

Eine Lösung

Wenn kein besprochener Fall zutrifft, dann schneiden einander die Gleichungen.