Was ist eine lineare Ungleichung?

Lineare Ungleichungen sind ähnlich wie lineare Gleichungen. Jede Variable darf also höchstens in der 1. Potenz vorkommen. Der einzige Unterschied zu den Gleichung liegt daran, dass statt dem Gleichheitszeichen = ein Ungleichheitszeichen <, \leq, >, \geq verwendet wird.

Ungleichungen können wahr oder falsch sein

Ungleichungen können gleich wie Gleichungen wahr oder falsch sein. Es ist klar, dass 4 < 5 eine wahre Aussage ist. Im Gegensatz dazu ist die Aussage 4 > 5 falsch. Betrachtet man die Ungleichung

2x > 4 ,

so sind alle Zahlen gesucht, welche man für x einsetzen kann, sodass die Ungleichung wahr ist. In diesem Fall muss gelten, dass x>2 ist. Die Lösungmenge ist also: \mathbb{L} = \{x \in \mathbb{R} | x > 2\}. Dies führt uns gleich zu den Rechenregeln. Wie darf man Ungleichungen umformen?

Rechenregeln

Man darf auf beiden Seiten einer Ungleichung dieselbe Zahl addieren und subtrahieren.

a \leq b \Rightarrow a + c \leq b + c

Die Zahl c kann größer (Addition), kleiner (Subtraktion) oder gleich Null sein.

 

Zwei gleichgerichtete Ungleichung dürfen addiert werden.

\begin{array}{rlr} a \leq b &\; \text{und} \; c \leq d &\Rightarrow a + c \leq b + d \\ a < b &\; \text{und} \; c \leq d &\Rightarrow a + c < b + d \end{array}

 

Eine Ungleichung darf mit einer nichtnegativen Zahl multipliziert werden.

a \leq b \; \text{und} \; c \geq 0 \Rightarrow ac \leq bc

Das Ungleichheitszeichen verändert sich nicht.

 

Wird eine Ungleichung mit einer negativen Zahl multipliziert (oder dividiert), so dreht sich das  Ungleichheitszeichen um.

a \leq b \; \text{und} \; c \leq 0 \Rightarrow ac \, {\color{red}{\geq}}  bc

Das Ungleichheitszeichen verändert sich. Es dreht sich um.

 

Wenn die Seiten der Ungleichung entweder beide positiv oder beide negativ sind, gilt: Bildet man auf beiden Seiten einer Ungleichung den Kehrwert, so dreht sich das Ungleichheitszeichen um.

a \leq b \Rightarrow \dfrac{1}{b} \leq \dfrac{1}{a}

 

Lösen von Ungleichungen in einer Variablen

Beispiel 1

Löse folgende Ungleichung in den reellen Zahlen.

\begin{array}{rll} 20x - 8 &\leq 3x + 4 &|  -3x \\ 17x -8 &\leq 4 &|+8 \\ 17x &\leq 4 &| :17 \\ x &\leq \dfrac{4}{17} &\end{array} \mathbb{L} = \{x \in \mathbb{R} | x \leq \dfrac{4}{17} \}

Zusammenfassung: Wir können hier so rechnen, als ob es sich um eine ‘normale’ Gleichung handelt.

Beispiel 2

Löse in den natürlichen Zahlen.

\begin{array}{rll} -2x+4 &\geq 2 &|  -4\\ -2x  &\geq -2 &|:(-2) \\ x &\leq 1 & \end{array}

Nun müssen wir noch die Lösungsmenge angeben. Achtung. Wir müssen die Ungleichung in den natürlichen Zahlen \{0,1,2,3, \dots\} lösen. Aus der Ungleichung erhalten wir, dass x  \leq 1 gelten muss. Somit erhalten wir für die Lösungsmenge \mathbb{L} = \{x \in \mathbb{N} | x \leq 1 \} = \{0,1\} .

Lösen von Ungleichungen in zwei Variablen

Wir wollen nun eine lineare Ungleichung in zwei Variablen x und y lösen. Die Vorgangsweise ist meist dieselbe. Wir lösen nach einer Variable auf (meistens y ) und versuchen die Lösung graphisch zu deuten und die Lösungsmenge anzugeben.

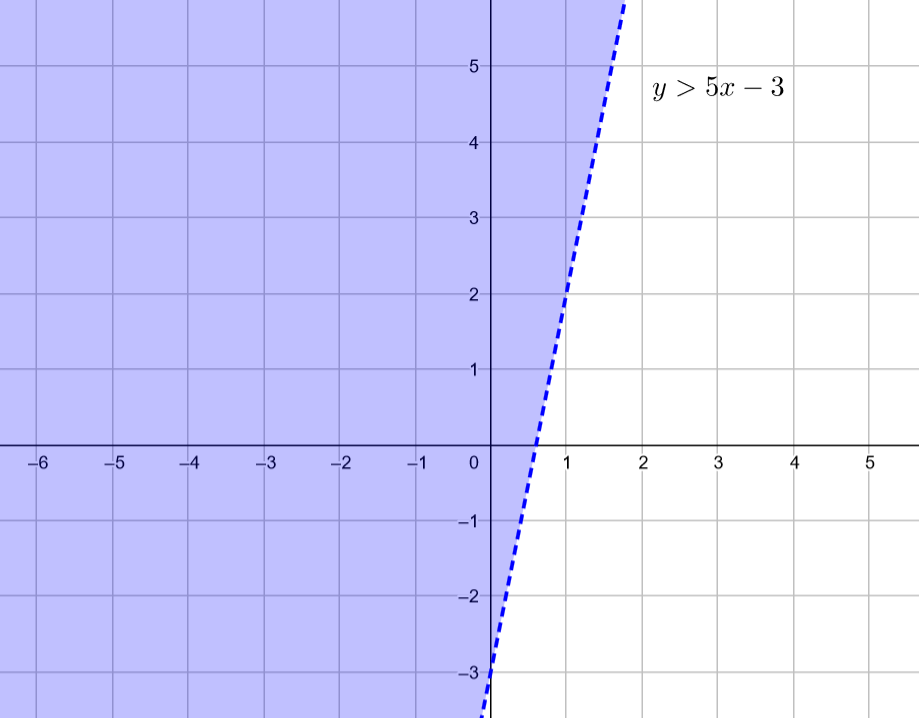
\begin{array} {rll} 10x - 2y &< 6 &| -10x \\ -2y &< -10x + 6 &| :(-2) \\ y &> 5x - 3 &\end{array}

Wenn wir anstatt dem Ungleichheitszeichen ein Gleichheitszeichen, wäre dies eine lineare Funktion, also eine Gerade. Diese Gerade ist im Bild strichliert dargestellt. Da aber die y-Werte alle größer als die Funktionswerte sein müssen, liegen die y-Werte alle überhalb der Gerade. Das Ungleichheitszeichen ist ein strikt-größer Zeichen (>) . Deswegen sind die Werte auf der Geraden nicht mehr dabei. Dies wird durch die strichlierte Linie gekennzeichnet. Da alle Punkte überhalb der Geraden in der Lösungsmenge enthalten sind, sind in der Lösungsmenge alles Punkte mit den Koordinaten (x,y) . Die Lösungsmenge würde man wie folgt angeben: \mathbb{L} = \{(x,y) \in \mathbb{R}^2 | y > 5x-3 \} .