Algebra und Geometrie
Quadratische Gleichungen
Eine allgemeine quadratische Gleichung lässt sich in der Form
a x^2 + b x + c = 0 darstellen, wobei a,b,c \in \mathbb{R} sind.
Lösungen der quadratischen Gleichung sind Zahlen, die man für x einsetzt, sodass man eine sinnvolle Gleichung erhält.
Beispiel
Betrachten wir die Gleichung 2x^2 - 2x = 4. Wir können diese Gleichung genau so wie oben dargestellt schreiben, indem wir die Gleichung geeignet umformen.
\begin{array}{lrl} &2x^2 - 2x =& 4 \; \vert \; -4 \\ \Leftrightarrow &2x^2 - 2x -4 =& 0 \end{array}.
In diesem Fall ist a = 2, b = -2 und c=-4 . In diesem Fall können wir für x zwei Werte einsetzen, sodass eine sinnvolle Gleichung entsteht.
1. Fall: x = -1
\begin{array}{rl} 2 \cdot \underbrace{(-1)^2}_1 \underbrace{- 2 \cdot (-1)}_2 -4 =& 0 \\ 2 \cdot 1 + 2 -4 =& 0 \\[1ex] 0 =& 0 \; \checkmark \end{array}2. Fall: x = 2
\begin{array}{rl} 2 \cdot \underbrace{(2)^2}_4 \underbrace{- 2 \cdot 2}_{-4} -4 =& 0 \\ \underbrace{2 \cdot 4}_8 + -4 -4 =& 0 \\ 0 =& 0 \; \checkmark \end{array}Wir sehen also, dass wir hier zwei Lösungen haben, die Lösungsmenge ist also gegeben durch \mathbb{L} = \{-1,2\} . Im Allgemeinen kann eine Lösung in den reellen Zahlen
- keine Lösung
- eine Lösung oder
- zwei Lösungen haben.
Dies hängt von der jeweiligen Gleichung ab.
Wie findet man die Lösungen ohne Probieren?
Bei einfachen Gleichungen wie x^2 = 4 \;(a=1, b=0, c=-4) kann man durch Wurzelziehen die Lösungen x_{1,2} = \pm 2 sehr schnell und einfach berechnen. Das geht auch mit der oben dargestellten allgemeinen Gleichung einer quadratischen Gleichung, wir müssen diese nur ein bisschen umformen.
Die Mitternachtsformel (Große Lösungsformel)
\begin{array}{rcll} ax^2+bx+c & = & 0 &| -c\\[1ex] ax^2+bx & = & -c&|{}\cdot 4a\\[1ex] 4a^2x^2+4abx & = & -4ac&| +b^2 \text{ (quadratische Ergänzung)}\\[1ex] (2ax)^2+2\cdot 2ax\,b + b^2 & = & b^2-4ac &|\text{ Umformen mit binomischer Formel}\\[1ex] (2ax+b)^2 & = & b^2-4ac &| \pm \sqrt{\quad}\\[1ex] 2ax+b & = & \pm\sqrt{b^2-4ac} &|-b\\[1ex] 2ax & = & -b \pm\sqrt{b^2-4ac} &|:(2a)\\[1ex] x_{1,2} & = & \dfrac{-b\pm\sqrt{b^2-4ac}}{2a}& \end{array}Diese Gleichung nennt man auch “Große Lösungsformel” oder “Mitternachtsformel”. Dadurch muss man lediglich die Werte für a,b,c einsetzen und erhält die Lösungen der quadratischen Gleichung.
Es gibt auch noch eine sog. “Kleine Lösungsformel”. Diese kann dann angewendet werden, wenn a = 1 gilt.
Wir verwenden dann aber andere Bezeichnungen: Aus ax^2+bx+c=0 wird mit
a = 1, b \rightarrow p, c \rightarrow q die Gleichung: x^2+px+q=0 .
Die kleine Lösungsformel
Die Lösungen dieser Gleichung können wir auch angeben, wenn wir in die “Mitternachtsformel” die passenden Variablen einsetzen:
\begin{array}{rcll} x_{1,2} & = & \dfrac{-b\pm\sqrt{b^2-4ac}}{2a}&| \; a = 1, b \rightarrow p, c \rightarrow q \\[2ex] x_{1,2} & = & \dfrac{-p\pm\sqrt{p^2-4q}}{2}&| \; \text{(Bruch auseinanderziehen)}\\[2ex] x_{1,2} & = & \dfrac{-p}{2}\pm\dfrac{\sqrt{p^2-4q}}{2}&| \; \text{(Nenner unter die Wurzel bringen)} \\[2ex] x_{1,2} & = & \dfrac{-p}{2}\pm \sqrt{\dfrac{p^2-4q}{4}}&| \; \text{(Bruch auseinanderziehen)} \\[2ex] x_{1,2} & = & \dfrac{-p}{2}\pm \sqrt{\dfrac{p^2}{4}-\dfrac{4q}{4}}&| \; \text{(Kürzen)} \\[2ex] x_{1,2} & = & - \dfrac{p}{2}\pm \sqrt{\left(\dfrac{p}{2}\right)^2-q}&\end{array}
Wann gibt es keine/ eine oder zwei Lösung(en) in den reellen Zahlen?
Wir haben im Kapitel Zahlenmengen gesehen, dass wir solange wir mit den reellen Zahlen arbeiten können, bis unter den Wurzeln negative Ausdrücke auftauchen. In beiden Lösungsformeln kommen auch Wurzelausdrücke vor. Diese Wurzelausdrücke bestimmen, ob es keine, eine oder zwei Lösung(en) gibt. Den Ausdruck unterhalb der Wurzel bezeichnet man als Diskiminante D .
| Gleichung | Lösungsformel | Wurzelausdruck | Diskriminante D |
|---|---|---|---|
| a x^2 + b x + c = 0 | x_{1,2} = \dfrac{-b\pm\sqrt{b^2-4ac}}{2a} | \sqrt{b^2-4ac} | b^2-4ac |
| x^2+px+q=0 | x_{1,2} = - \dfrac{p}{2}\pm \sqrt{\left(\dfrac{p}{2}\right)^2-q} | \sqrt{\left(\dfrac{p}{2}\right)^2-q} | \left(\dfrac{p}{2}\right)^2-q |
Lösungsfälle
Es gibt in den reellen Zahlen
- keine Lösung, wenn D < 0 ,
- eine Lösung, wenn D = 0 und
- zwei Lösungen, wenn D > 0 ist.
In den komplexen Zahlen gibt es immer so viele Lösungen, wie der Grad der höchsten vorkommenden Potenz. Bei quadratischen Gleichungen gibt es in den komplexen Zahlen also immer zwei Lösungen.
Beispiel
Betrachte die quadratische Gleichung \dfrac{1}{2}x^2 - x + \alpha = 0 .
Wir wollen den Wert von \alpha so angeben, dass diese quadratische Gleichung keine, eine und zwei Lösung(en) hat.
Die Anzahl der Lösungen sind abhängig von der Diskriminante D = b^2 - 4ac . In unserem Beispiel gilt: a = \dfrac{1}{2}, b = -1 und c = \alpha .
1. Fall: D=0 (eine Lösung)
\begin{array}{rl} D =& b^2 - 4ac \\ =& (-1)^2 - 4 \cdot \dfrac{1}{2} \cdot \alpha \\ =& 1 - 2 \alpha \end{array}\begin{array}{lrll} &0 = & 1 - 2 \alpha &| +2\alpha \\ \Leftrightarrow &2 \alpha =& 1 &| :2 \\ \Leftrightarrow & \alpha=&\dfrac{1}{2}& \end{array}
Wenn wir für \alpha = \dfrac{1}{2} einsetzen, ist die Diskriminante 0 .
Grafisch ist eine Lösung immer ein Schnittpunkt des Graphen mit der x-Achse. Da wir eine Lösung haben, haben wir genau einen Schnittpunkt (Berührpunkt) mit der x-Achse.
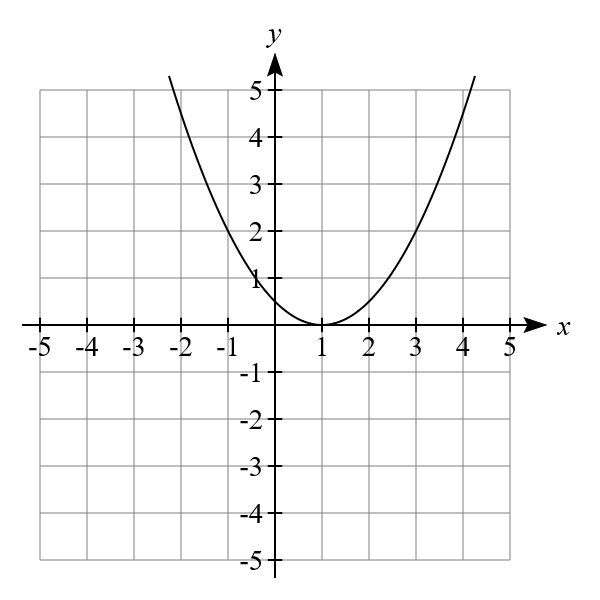
Für die anderen beiden Fälle müssen wir nur noch Werte von \alpha > \dfrac{1}{2} und \alpha < \dfrac{1}{2} betrachten.
Quadratische Gleichung – eine Lösung (Nullstelle)
2. Fall: D<0 (keine Lösung)
Wir sehen, dass für \alpha > \dfrac{1}{2} die Diskriminante D = 1 - 2 \alpha <0 ist. Somit haben wir hier keine Lösung. Im Koordinatensystem wäre der Graph nach oben verschoben, sodass wir keinen Schnittpunkt mit der x-Achse haben. Wie weit wir den Graphen nach oben verschieben, hängt von Wert von \alpha ab.
3. Fall: D>0 (zwei Lösungen)
Andererseits erkennt man, dass für \alpha < \dfrac{1}{2} die Diskriminante D = 1 - 2 \alpha > 0 ist. Somit haben wir hier zwei Lösungen. Im Koordinatensystem wäre der Graph nun nach unten verschoben, sodass wir zwei Schnittpunkte mit der x-Achse haben. Wie weit wir den Graphen nach unten verschieben, hängt von Wert von \alpha ab.