Algebra und Geometrie

 

Am häufigsten werden Vektoren als Pfeile im Koordinatensystem (2D oder 3D) eingeführt. Dabei beschreiben alle Pfeile, die

• gleich lang,
• parallel und
• gleichorientiert sind, denselben Vektor.

Dies bedeutet, dass ein Vektor unabhängig vom Anfangspunkt ist.

Wie zeichnet man eine Vektor?

Wir wollen als Beispiel den Vektor \vec{a} = \left( \begin{matrix}{\color{red}{ 2}}\\ {\color{blue}{3}}\end{matrix}\right) zeichnen. Wir gehen wie folgt vor:

 

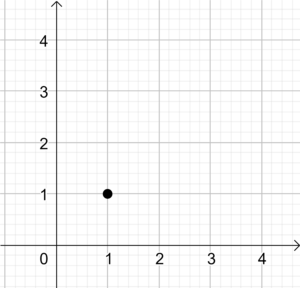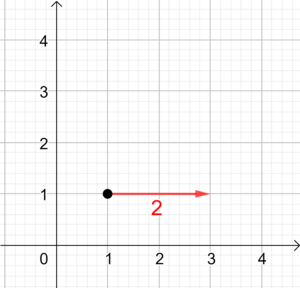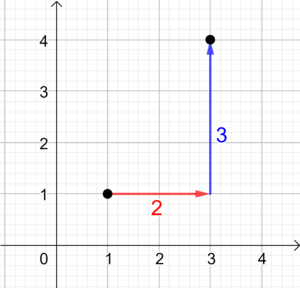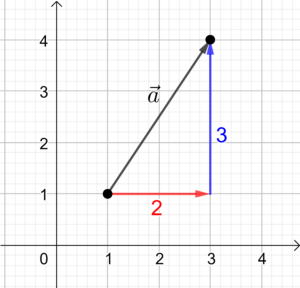Suche dir einen Anfangspunkt aus.	Zeichne die erste Komponente (2) des Vektors in x-Richtung.	Zeichne anschließend die zweite Komponente (3) des Vektors in y-Richtung.	Verbinde Anfangs- und Endpunkt. Der Pfeil zeigt Richtung Endpunkt.

Berechnung von Vektoren aus Anfangs- und Endpunkt

Ein Vektor \vec{u} , welcher vom Punkt A = \left( \begin{matrix} a_1 \\ a_2 \end{matrix}\right) zum Punkt B= \left( \begin{matrix} b_1 \\ b_2 \end{matrix}\right) zeigt, hat die Darstellung

\vec{u} = \overrightarrow{AB}  = \left( \begin{matrix} b_1 - a_1 \\ b_2 - a_2\end{matrix}\right) . Die Einträge werden also Zeilenweise voneinander subtrahiert. Die Rechenregel, um den Vektor zwischen zwei Punkten zu bekommen, lautet wie folgt:

\text{Vektor} = \text{Spitze} - \text{Anfang} .

Möchte man, dass der Vektor \vec{v} von B nach A zeigt, so rechnet man auch wieder Spitze minus Schaft, also \vec{v}  = \overrightarrow{BA}= \left( \begin{matrix} a_1 - b_1 \\ a_2 - b_2\end{matrix}\right) . Beide Vektoren sind in untenstehender Abbildung dargestellt. Sie sind gleich lang und parallel, aber blicken in eine andere Richtung.

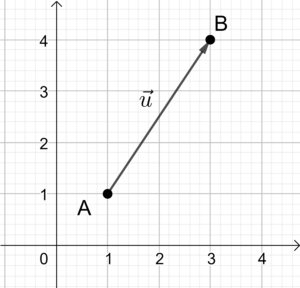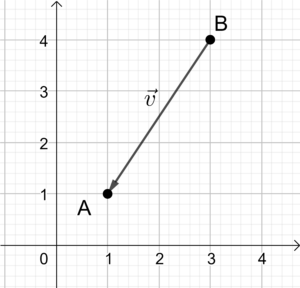\vec{u} = \overrightarrow{AB}  = \left( \begin{matrix} b_1 - a_1 \\ b_2 - a_2\end{matrix}\right) .	\vec{v}  = \overrightarrow{BA}= \left( \begin{matrix} a_1 - b_1 \\ a_2 - b_2\end{matrix}\right)

Unterschied Ortsvektor und Richtungsvektor

Ortsvektor

Ortsvektoren haben als Anfangspunkt immer den Nullpunkt (0,0) . Deswegen sind die Komponenten des Ortsvektors immer gleich wie die Komponenten des Punktes, zu welchen er zeigt. Es ist aber auf die unterschiedliche Schreibweise zu achten.

Betrachten wir den Punkt C = (2,3) . Der Ortsvektor \vec{w} zum Punkt C hat die Koordinaten

\vec{w} =\overrightarrow{OP}= \text{Spitze} - \text{Anfang} = \left(\begin{matrix} 2 - 0 \\ 3 - 0 \end{matrix} \right)= \left( \begin{matrix}  2  \\ 3 \end{matrix} \right) .

Jeder Punkt im Koordinatensystem kann als Ortsvektor aufgefasst werden. Dadurch kann man \text{Vektor} = \text{Spitze} - \text{Anfang} auch wie folgt formulieren:

\text{Vektor} = \text{Ortvektor der Spitze} - \text{Ortsvektor des Anfangs} .

Richtungsvektor

Richtungsvektoren können beliebige Anfangspunkte haben, auch den Nullpunkt (0,0) . Das heißt, dass Ortsvektor spezielle Richtungsvektoren darstellen. Jeder Ortsvektor ist ein Richtungsvektor, aber nicht jeder Richtungsvektor ist ein Ortsvektor.

Beispiel

Gegeben sind die beiden Punkte A = (-2,5) und B = (3,2) . Berechne den Richtungsvektor \vec{v} von A nach B .

\vec{v} = \overrightarrow{AB} = \overrightarrow{OB} - \overrightarrow{OA} = \left( \begin{matrix} 3 \\ 2 \end{matrix} \right) - \left( \begin{matrix} -2 \\ 5 \end{matrix} \right) = \left( \begin{matrix} 3 - (-2) \\ 2 - 5 \end{matrix} \right) = \left( \begin{matrix} 3 +2\\ 2-5 \end{matrix} \right)  = \left( \begin{matrix} 5 \\ -3 \end{matrix} \right) .