Das wichtigste auf einem Blick

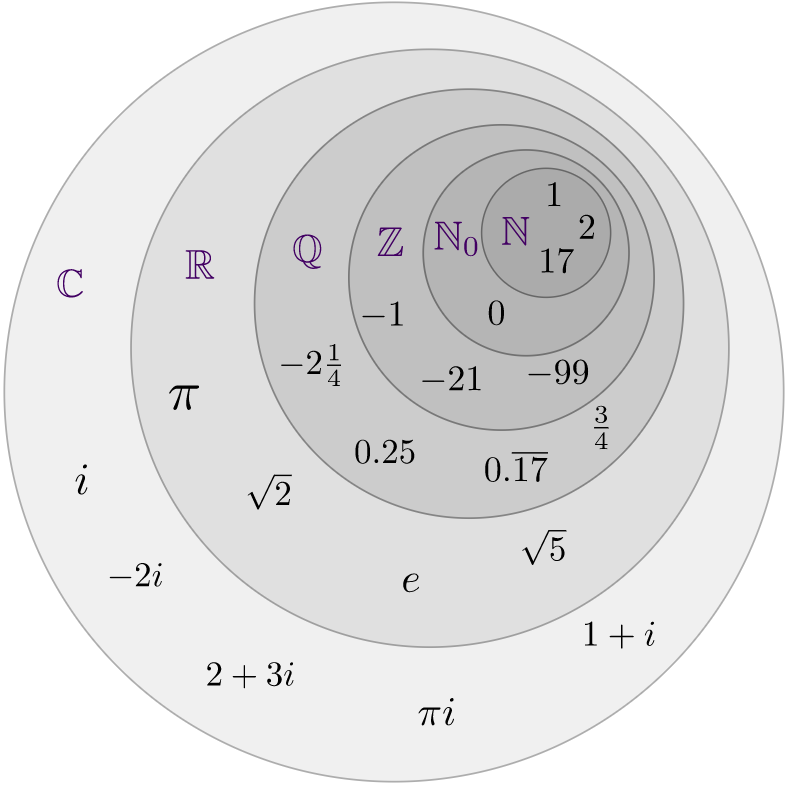
Die wichtigsten Eigenschaften lassen in in Form des angeführten Bildes erläutern. Das Bild ist wie folgt zu lesen:

Jede innere Menge ist auch in den äußeren enthalten. Das bedeutet: Alle natürliche Zahlen sind in der Menge der ganzen Zahlen, in der Menge der rationalen Zahlen, in der Menge der reellen Zahlen und in der Menge komplexen Zahlen enthalten. Mathematisch formuliert: \mathbb{N} \subset\mathbb{Z} \subset\mathbb{Q} \subset\mathbb{R} \subset\mathbb{C}

Beispiel

Zu welcher Zahlenmenge gehört die Zahl -2,\dot{8}. Da diese Zahl negativ ist, kann es keine natürliche Zahl sein. Da sie eine Dezimalzahl ist, ist es auch keine ganze Zahl. Die Zahl ist eine unendliche periodische Dezimalzahl, also eine rationale Zahl \mathbb{Q} . Die rationalen Zahlen sind aber auch in den reellen und komplexen Zahlen enthalten. Somit ist die Zahl -2,\dot{8} eine rationale, reelle und eine komplexe Zahl.

Wo sind die irrationalen Zahlen?

Die irrationalen Zahlen sind hier nicht eingezeichnet. Die befinden sich außerhalb des \mathbb{Q}-Kreises in den reellen Zahlen. Jede irrationale Zahl ist eine reelle und eine komplexe Zahl.

Besonderheit

In der Grafik ist auch die Menge \mathbb{N}_0 eingezeichnet. Je nach Schulbuch oder Fachliteratur findet man die Mengen \mathbb{N}_0 = \{0,1,2,3, \dots \} und \mathbb{N} = \{ 1,2,3, \dots\}, weil die Rolle der Zahl 0 unterschiedlich aufgefasst ist. Also nicht verwirren lassen, manchmal ist die Zahl 0 bei den natürlichen Zahlen dabei und manchmal nicht.