Was ist über chaotisches Verhalten?
In der Physik spricht man von deterministischem Chaos, wenn kleine Änderungen der Anfangsbedingungen große Änderungen des Gesamtsystems zur Folge haben. Die Veränderungen geschehen zwar nach vorher festgelegten Regeln (deterministisch), erscheinen aber zufällig. Im alltäglichen Sprachgebrauch ist in diesem Zusammenhang häufig die Rede vom sog. Schmetterlingseffekt. Dieser wurde eher zufällig vom Meteorologen Edward N. Lorenz entdeckt. Um Rechenzeit einzusparen, entschloss er sich die letzten Dezimalstellen der Anfangsbedingungen wegzulassen. Diese wichen um weniger als 10^{-4} voneinander ab. Zu seiner Überraschung resultierte diese als unerheblich erachtete Kleinigkeit in völlig unterschiedlichen Ergebnissen.
Das logistische Wachstum
Man stelle sich folgende Situation vor: In einer weit entfernten Galaxie gibt es eine unbekannte Art des Lebens, welche auf mehrere Sonnensystemen verteilt lebt. Die dort Lebenden pflanzen sich natürlich auch fort. Da Volkszählungen durch die großen Enternungen nur sehr schwer durchzuführen sind, möchte das wissenschaftliche Gremium der Galaxie die Bevölkerungsgröße modellieren.
Ein erster Vorschlag ist, dass die Bevölkerung jedes galaktische Jahr um eine gewissen Anteil r anwächst. Das heißt, dass die Bevölkerung im Vergleich zum Vorjahr immer um den Faktor r größer wird.
In der Sprache der Mathematik schreibt man dies in kontinuierlicher Form als Differenztialgleichung \dot{x} = r \cdot x mit Lösung x(t) = x_0 \cdot e^{rt} . Dieses Modell beschreibt eine Population zu Beginn ziemlich gut, da die Bevölkerung in dieser Zeit auchschnell anwächst. Jedoch sieht dieses Modell keine obere Grenze vor – das heißt, dass die Anzahl der Lebewesen unbeschränkt anwachsen könnte. Dies ist auf Grund der Beschränktheit von Ressourcen und Lebensraum nicht realistisch. Aus diesem Grund muss in die Differentialgleichung eine obere Grenze eingeführt werden. Eine solche Differentialgleichung sieht dann so aus: \dot{x} = r \cdot x \cdot (1-\dfrac{x}{K}) , wobei K die obere Grenze darstellen soll. Diese Differentialgleichung nennt man logistische Differentialgleichung. Sie besitzt eine analytische Lösung. Die skalierte Version ist von der Struktur gleich, aber es kommen keine Konstanten vor. Dabei werden die Einheiten so verändert, dass möglichst wenige Konstanten vorkommen. Man definiert neue Variablen N = \dfrac{x}{K} (neue dimensionslose Populationsgröße) und \tau = r \cdot t (neue dimensionslose Zeiteinheit). Betrachten wir zunächst die linke Seite und setzen unsere neuen Variablen ein. Bei der Ableitung müssen wir die Kettenregel verwenden.
\dot{x} = \dfrac{\mathrm{d}x(\tau (t))}{\mathrm{dt}} = K \cdot \dfrac{\mathrm{d}N(\tau(t))}{\mathrm{dt}} = K \cdot \dfrac{\mathrm{d}N}{\mathrm{d \tau}} \dfrac{\mathrm{d \tau}}{\mathrm{dt}} = K \cdot \dot{N} \cdot r
Die rechte Seite ändert sich zu
r \cdot x \cdot (1-\dfrac{x}{K}) = r \cdot K \cdot N \cdot (1-N) .
Jetzt können wir beide Seiten gleichsetzen und erhalten
K \cdot \dot{N} \cdot r = r \cdot K \cdot N \cdot (1-N) .
Nach dem kürzen bleibt noch die skalierte Form der Differientialgleichung übrig
\dot{N} = N \cdot (1-N) .
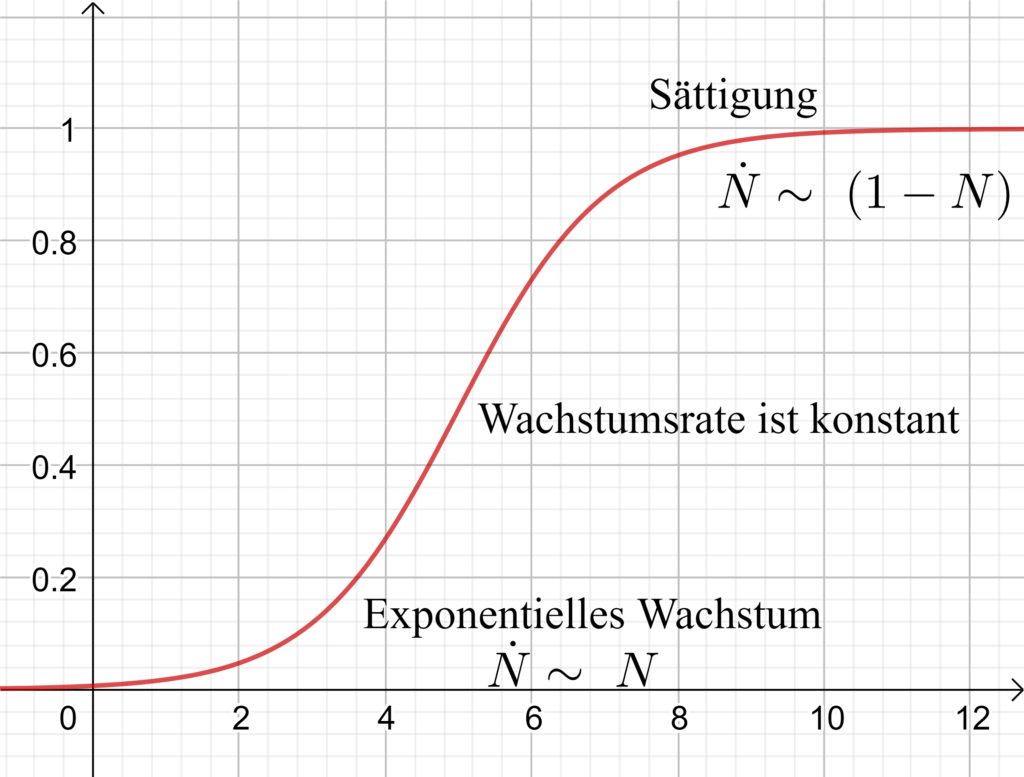
Dadurch ergibt sich also obere Grenze der Population der Wert 1. Hier ist spannend, dass der Parameter r aus dem Modell verschwindet. Dieses Modell verhält sich im kontinuierlichen Fall genau so, wie es erwünscht ist. Für den Fall, dass es zu viele Lebewesen gibt, also N > 1, so ist die Änderung \dot{N} < 0 , sodass die Populaton abnimmt. Ist die Population zu klein (N < 1), dann ist \dot{N} > 0 und die Population wächst weiter. Im nebenstehenden Bild erkennt man die Abhängigkeiten.
Jetzt kann man sich berechtigterweise die Frage stellen, wo das Chaos bleibt. Das Modell macht genau das, was es soll und es gibt keine Probleme. Die Probleme entstehen dann, wenn man das Modell in der ursprünglichen diskreten Form verwendet.
Diskrete logistische Gleichung - Das Chaos beginnt
Es mag zwar vielleicht zunächst etwas komisch klingen, dass es einen Unterschied macht, ob man mit diskreten oder kontinuierlichen Größen rechnet – aber es macht einen Unterschied. Die diskrete logistische Gleichung sieht ähnlich aus:
x_{k+1} = r \cdot x_k \cdot (1- \dfrac{x_k}{K})
Wir versuchen hier auch skalierte Größen zu verwenden. Wir ersetzen N_k = \dfrac{x_k}{K} und erhalten
N_{k+1} = r \cdot N_{k} \cdot (1- N_k)
Es lässt sich erkennen, dass die Zeit nicht skaliert werden kann. Dadurch bleibt ein Parameter in der Gleichung erhalten – dieser bestimmt maßgeblich das Verhalten des Systems. Im Unterschied zum kontinuierlichen Modell muss für alle k gelten, dass
0 < N_k <1,
da die Population niemals negativ sein kann. Diese Tatsache schränkt auch die Werte für r . Da die Gleichung eine auf dem Kopf stehende Parabel mit einem Hochpunkt darstellt, muss gewährleistet sein, dass auch folgende Generationen zwischen 0 und 1 sind. Dies führt zur Bedingung
0 < r < 4 .
Was passiert mit der Population bei verschiedenen Werten von r .
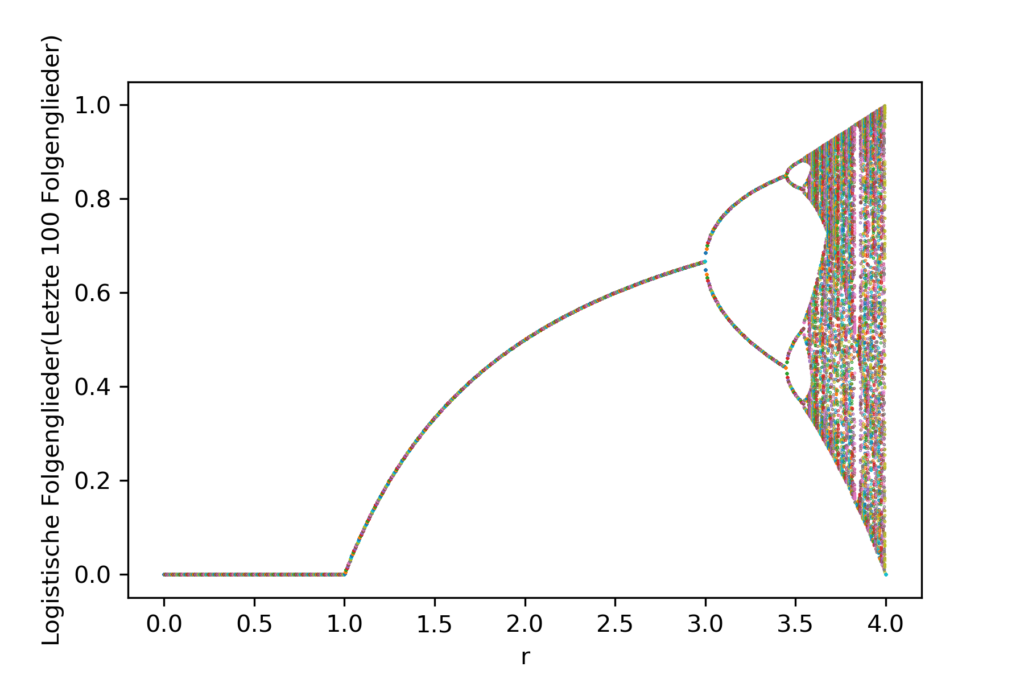
Im Diagramm sind die jeweilgen endlichen Populationsgrößen, also die Grenzwerte, für die verschiedenen Werte von r dargestellt. Im Bereich von 0<r<3 ist nichts auffällig – es gibt jeweils einen Grenzwert. Für 0<r<1 stirbt unsere Population in der fernen Galaxie leider aus. Interessant wird es für Werte 3<r<4 – diese kann man sich durchaus genauer ansehen. Untenstehend findet ihr die Python-Datei, um dieses Diagramm zu zeichnen.
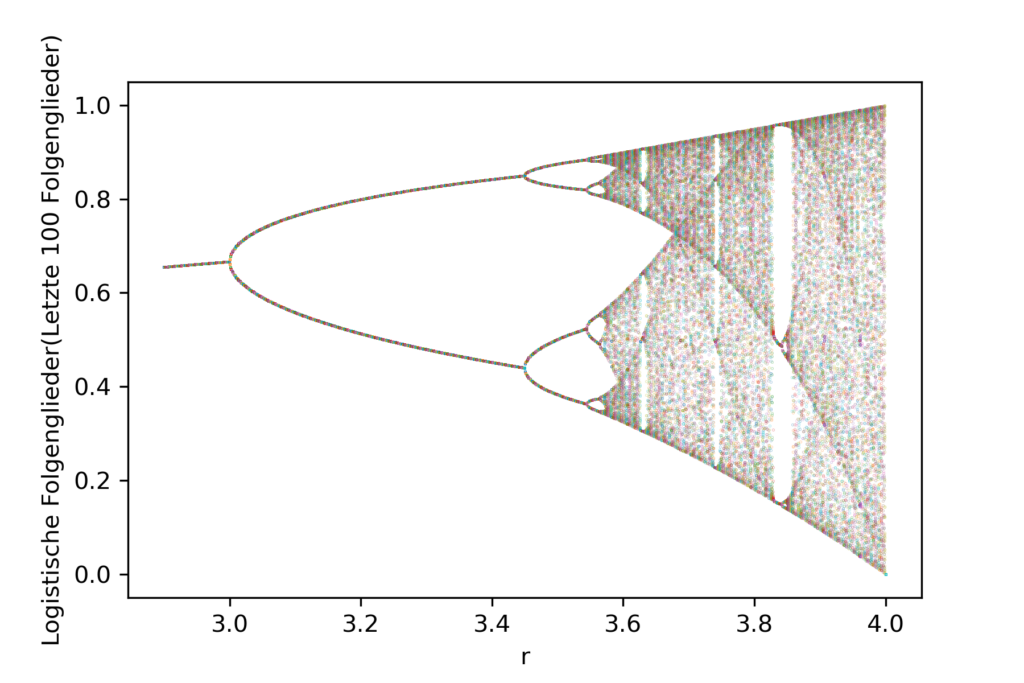
HIer erkennt man, dass die Population für Werte r>3 immer zwischen zwei Werten hin und her springt – und das nach jedem Jahr. Es wird sogar noch chaotischer. Bei Werten von r \sim 3,50 werden abwechselnd vier verschieden Werte für unsere galaktische Population angenommen. Man stelle sich das einmal für ein Land wie Österreich vor. Im aktuellen Jahr 8 \, \mathrm{Mio.} EinwohnerInnen – im nächsten Jahr nur mehr 4 \, \mathrm{Mio.} und dann wieder 6 \, \mathrm{Mio.} EinwohnerInnen.
Für Werte r>3,54 werden es sogar immer mehr Häufungspunkte – zuerst 8 , dann 16, 32,64, …. Die Intervalle werden immer kleiner und kleiner. In diesem Zusammenhang ist interessant, dass das Verhältnis der Breite aufeinanderfolgender Intervalle, in welchen 8 , dann 16, 32,64, … Häufungspunkte vorkommen, sich einer konstanten Zahl – der Feigenbaum-Konstante annähern:
\delta = 4,6692 … .
Das Ganze mag zwar schon chaotisch wirken, aber es gibt noch eine Regelmäßigkeit. Ab Werten von r \sim 3,57 beginnt das richtige Chaos – es gibt keine Regelmäßigkeiten mehr. Dies erkennt man auch im Bild durch die willkürliche Punktwolke. Es zeigen sich aber immer wieder Bereiche, in welchen sich die Punkte bei gewissen Punkten häufen – diese sind dort, wo es viele weiße Flächen gibt.
Es hat sich gezeigt, dass sich chaotischen Verhalten schon bei sehr einfachen Gleichungen äußern kann. Spannend ist auch der Zusammenhang zur Mandelbrot Menge, welche sich mit komplexen Zahlen beschäftigt. Diese Menge ist auch im Titelbild dargestellt. Kleine Veränderungen können große Auswirkungen haben – dies zeigen auch beide Diagramme. Ein weiteres interessantes Beispiel ist auch das Doppelpendel, welches auch vielleicht auch noch analysiert und modelliert wird.
Quellen
https://de.wikipedia.org/wiki/Logistische_Gleichung